
Y Ax 2 Bx C のグラフのかき方 事前テスト解答例 Kyokuryo Math
Y=ax² の形になる、 「2乗に比例する関数」 でしか 使えない裏技なのですが、 (yの増加量)÷(xの増加量) よりも速いので、 基本を理解した人には オススメの公式なのです。 <ひとこと> なお、 (yの増加量)÷(xの増加量) 2次関数 y=ax2乗bxcのグラフと x軸との共有点の数は,2次方程式 ax2乗bxc=0の解の公式 x=2a分−b±√b2乗−4acを用いて求める。 根号の中が正のとき,根号の中が 0のとき,根号の中が負のとき,2次関数 y=ax2乗b xcのグラフと x軸との共有点の数はそれぞれいくつになるか「正のとき〜,0のとき〜,負のとき〜。 」の形で答えなさい。 これの答えを教 数学 2次関
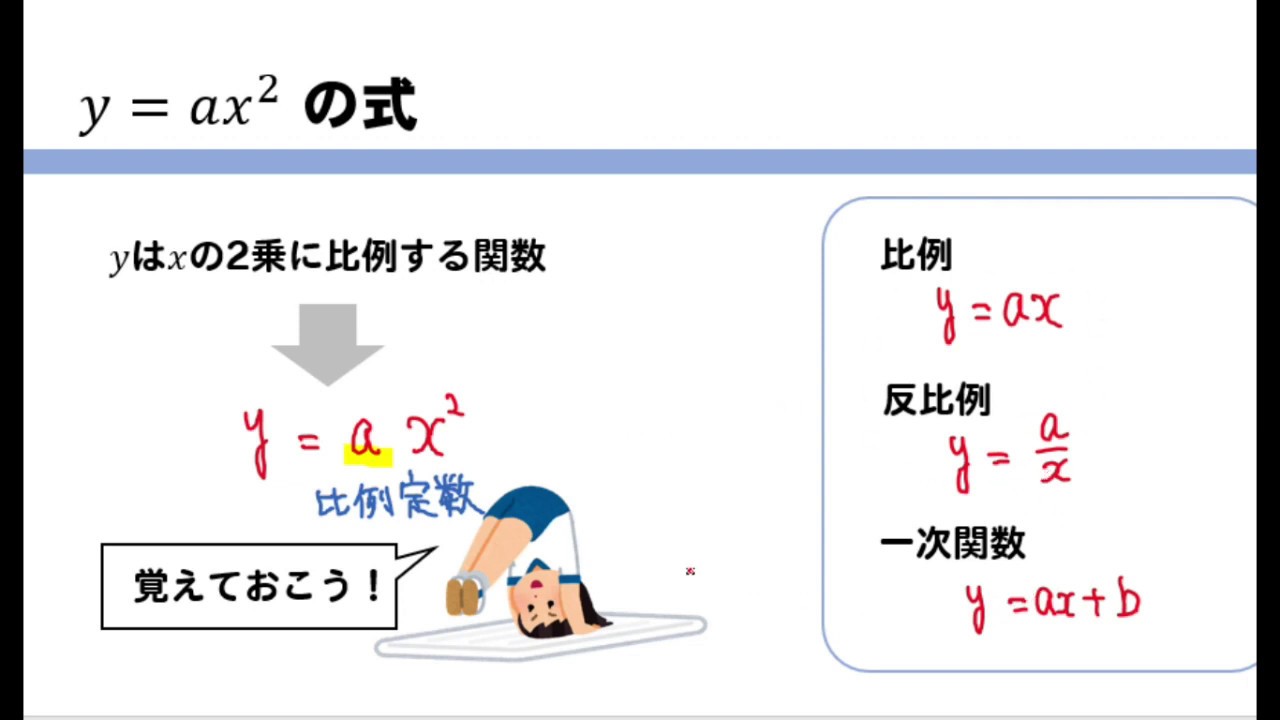
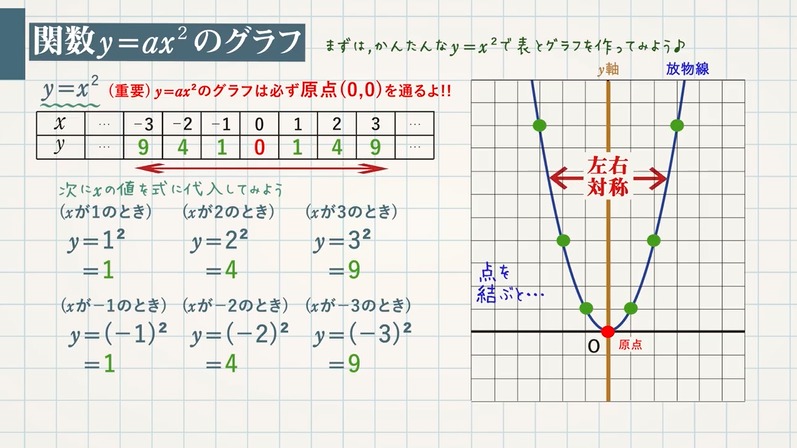
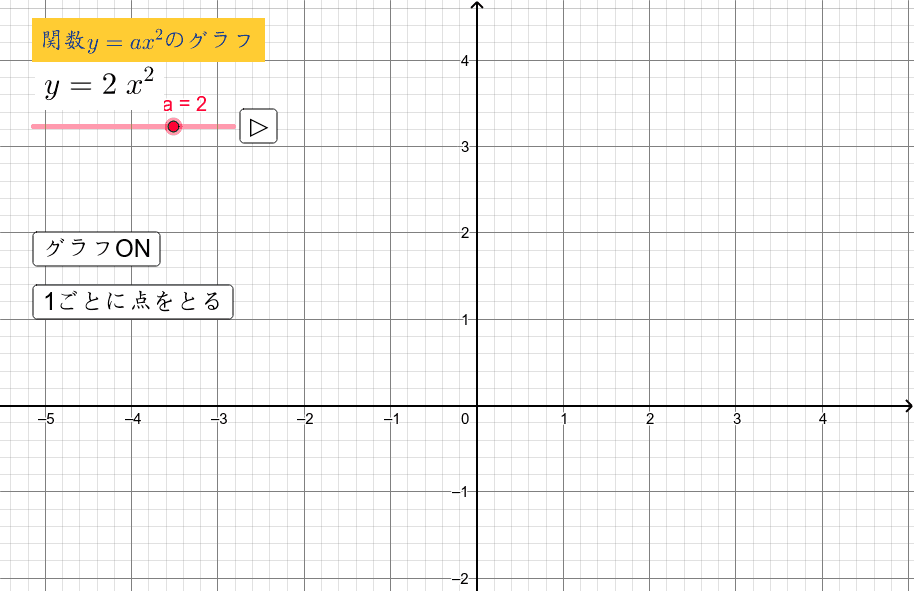
Y=ax二乗のグラフ
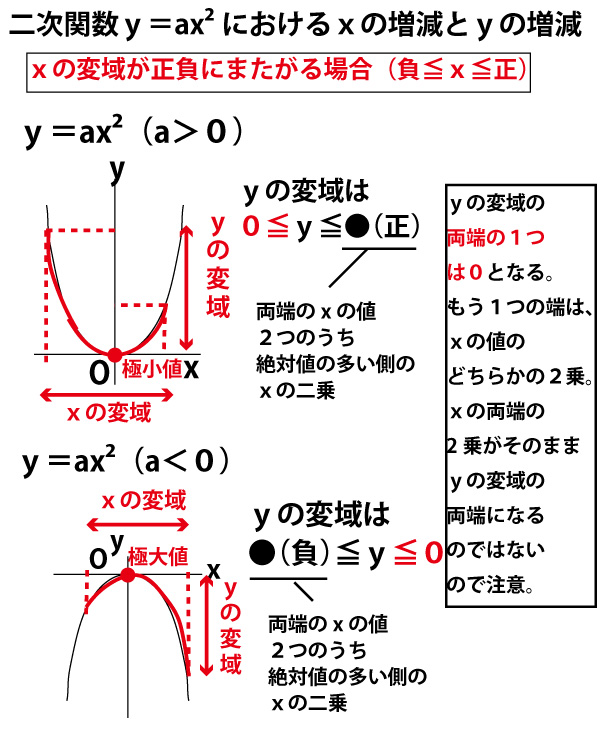
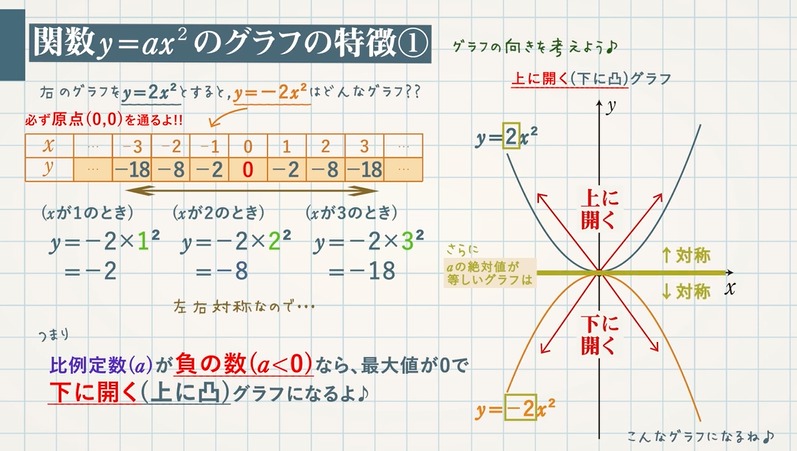
Y=ax二乗のグラフ-二乗に比例(ひれい)とは、y=ax 2 の式のように「yの値がxの2乗に比例する」ことです。aを比例定数(ひれいていすう)といいます。二乗に比例するグラフを下図に示します。 比例定数aが正、負のときでグラフの向きが変わる点に注意しましょう。中3数学。2乗に比例する関数(y = ax²)の「変域」を求めなさい。うわ、変域って何? 頂点が最小? 分からん(ガクッ)倒れ込む中学生。立て、立つんだトォォォォ~ッ! オール5家庭教師、見参ッ! グイグイ成績が上がる数学のコツ。無料サイトだ。
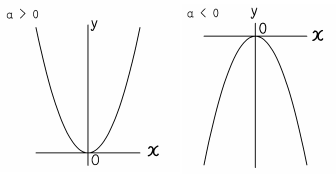
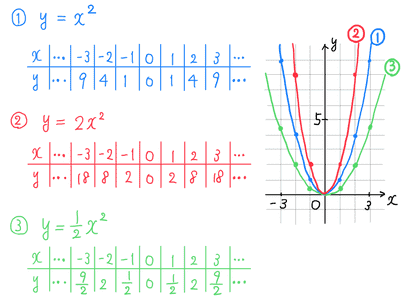
2乗に比例する関数 グラフ
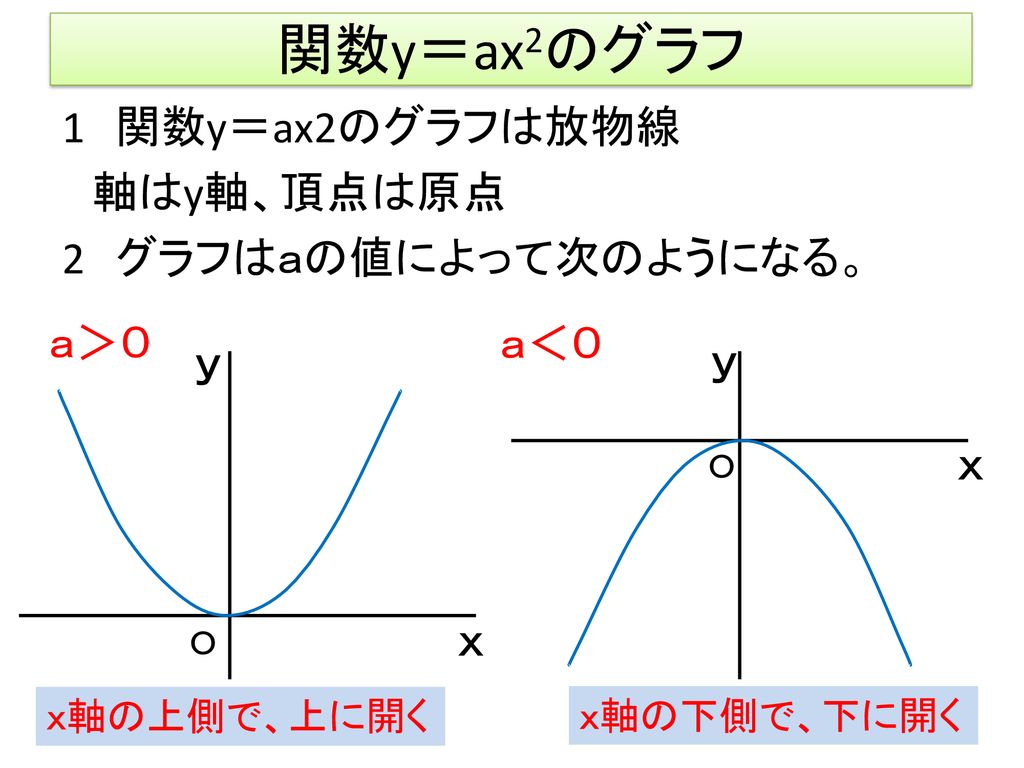
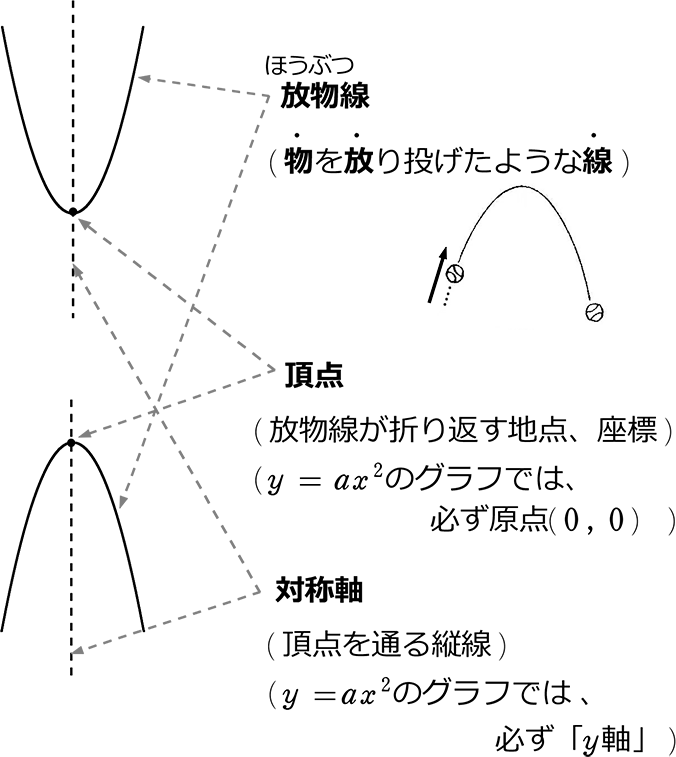
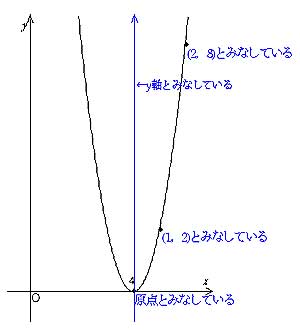
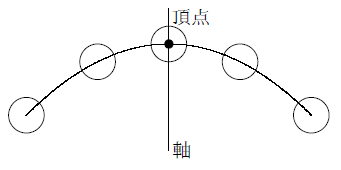
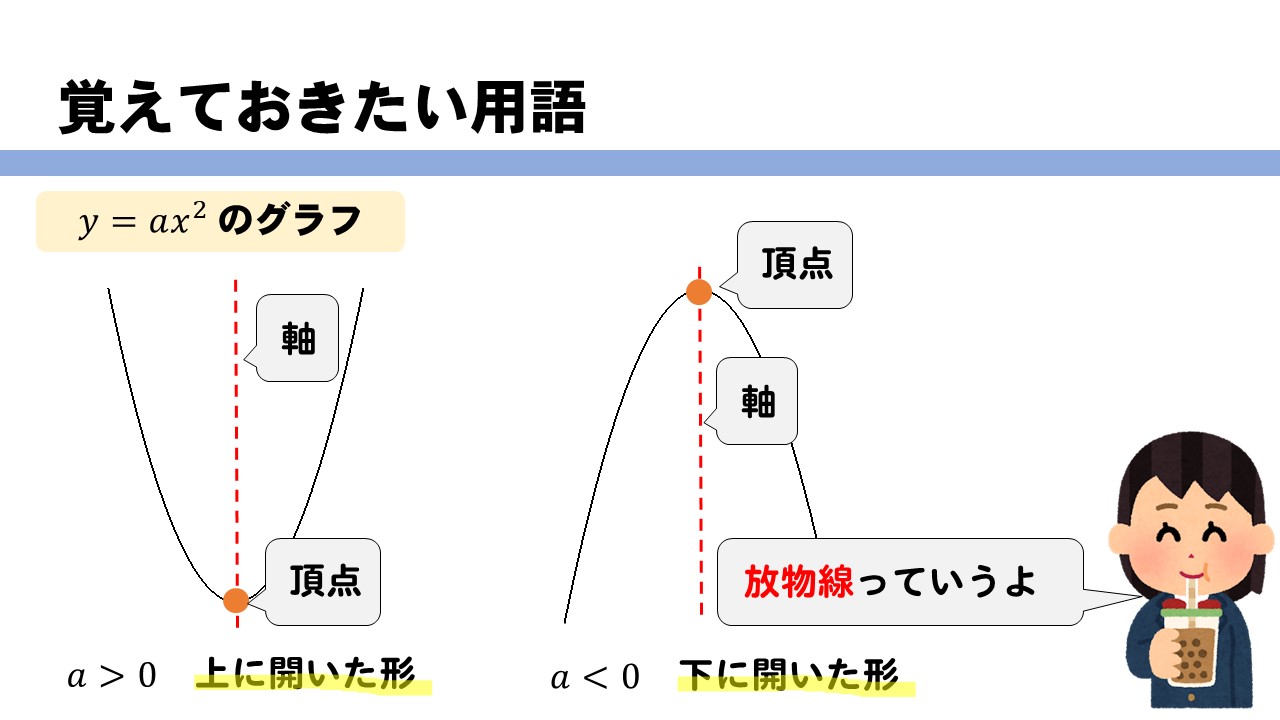
この記事ではこんなことを書いています 最小二乗法によってデータの回帰直線を求める方法を丁寧に解説していきます。 まずは、最小二乗法とは何かということを数式を使わずにざっくりと理解します。 その後、最小二乗法の式の導出を途中の計算式を省略せずに紹介します。 最後に、となるから, y=ax2 のグラフは 軸に関して対称であるといえます。 したがって, y軸は放物線 =ax2 の軸(対称軸)とよばれます。な お,一般に放物線とその軸との交点を頂点といい,y=ax2 のグラフ では原点が頂点となります。A,Bの座標が次のそれぞれの場合において、y=ax 2 のグラフが線分AB(両端を含む)と交わるようなaの値の範囲を求めよ。 A(2,1), B(2,8) A(4, 4), B(4, 8) A(3, 1), B(3, 9) 図の放物線lはy= 1 2 x 2 の グラフで、放物線mはy=ax 2 のグラフである。lとmがx軸に平行な直線nと交わる点をそれぞれA, Bとする。Aのx座標が
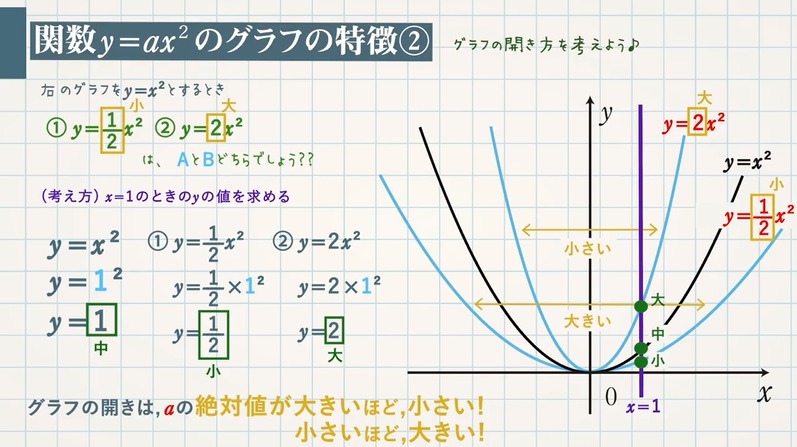
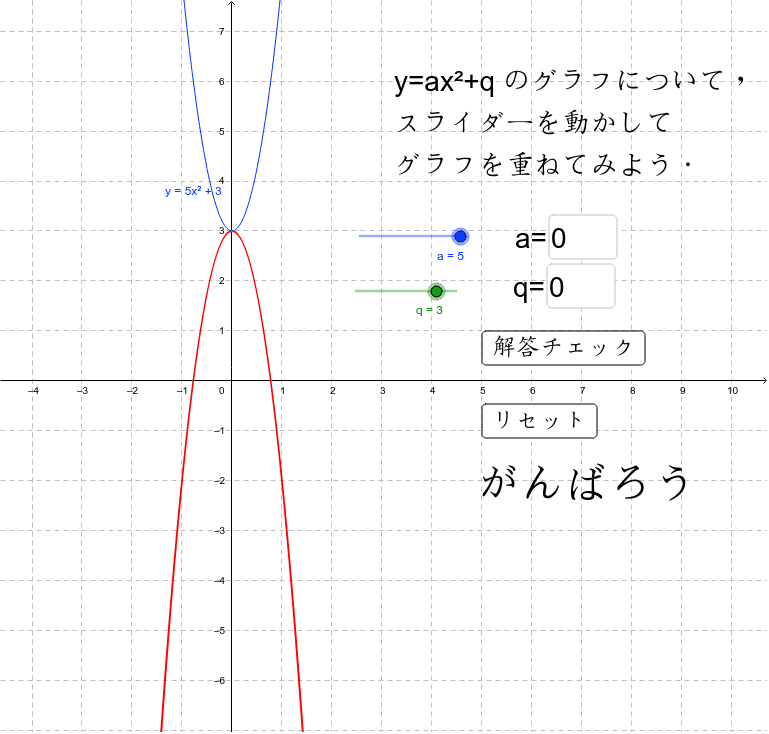
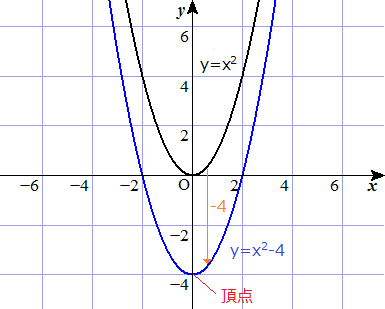
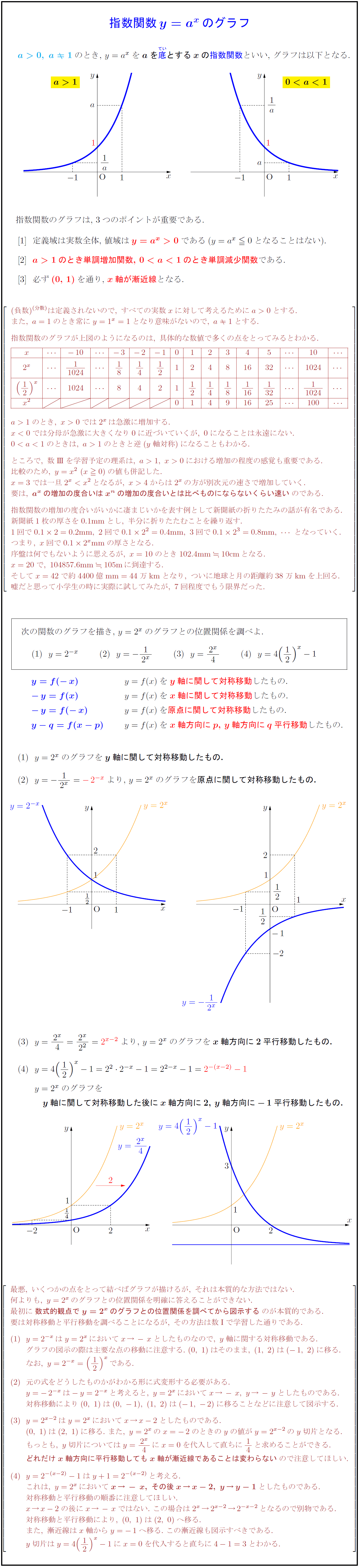
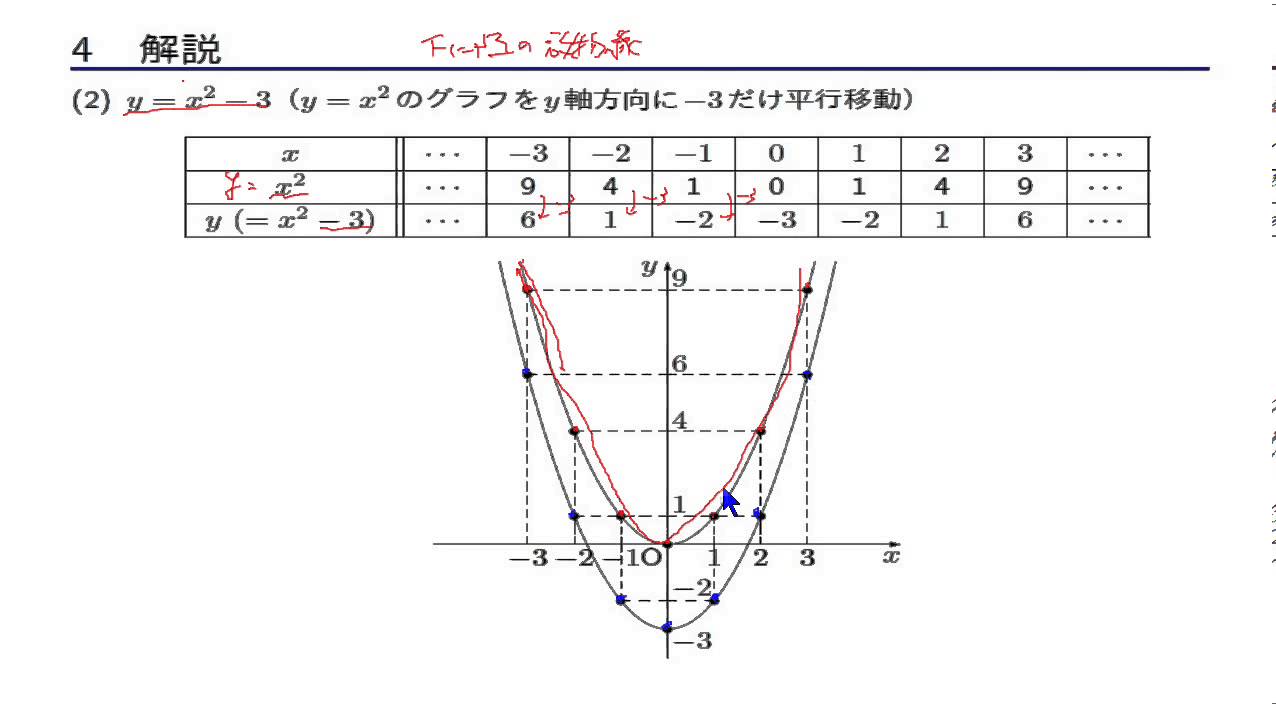
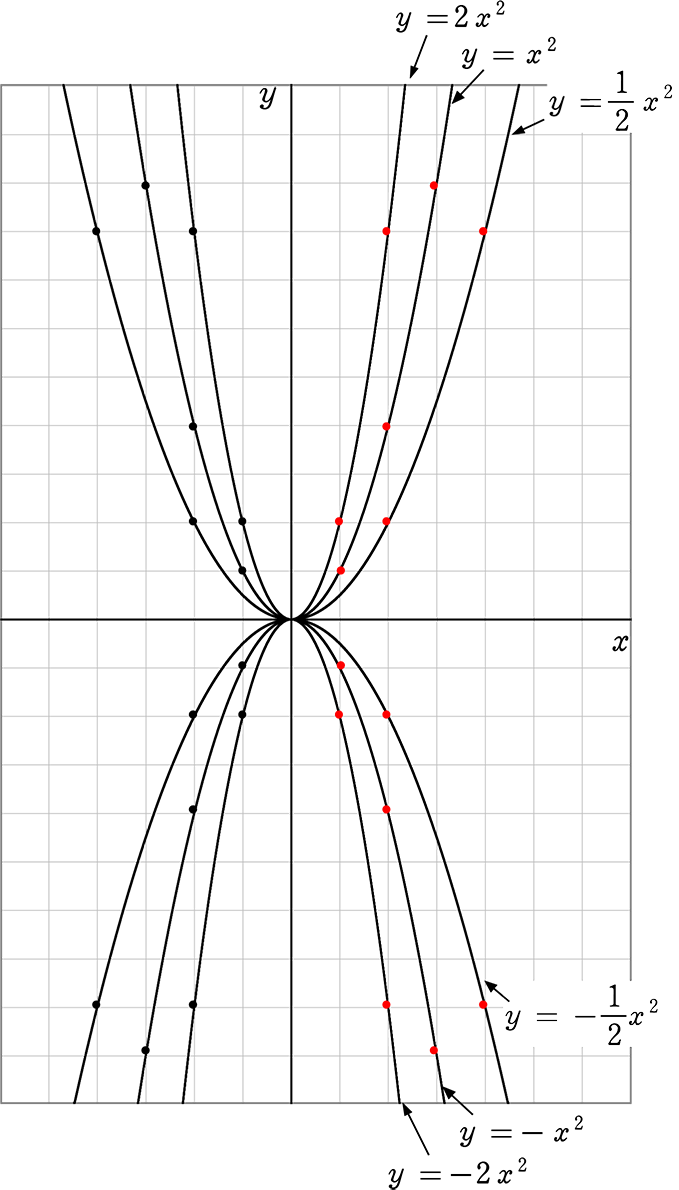
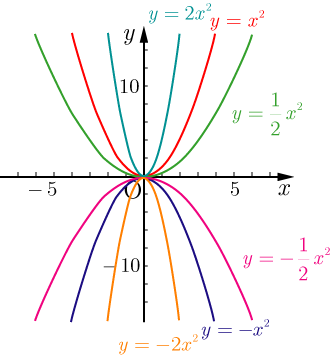
しかし、 ここで行った式変形(平方完成のやり方)を理解して、自分でできるようになっておく必要はあります 。 このことから、二次関数 y = ax2 bx c y = a x 2 b x c のグラフは、 b, c がどんな実数であっても、 y = ax2 y = a x 2 と同じ形になることが分かります。 y = ax2 y = a x 2 のグラフを 「放物線」といいました が、 y = ax2 bx c y = a x 2 b x c のグラフも 放物線つまり、 y = x2 y = x 2 y = x2 y = x 2 を連立して解くと、交点の座標が求まるということです。 y y を消せば、 x2 = x2 x 2 = x 2 という 2 2 次方程式になります。 さきほど解いた 2 2 次方程式と同一のものですね。 交点 とは、上の 2 2 つの式を満たす x x と y y下のグラフが\(y=3x^{2}\)です。 一方、下のグラフが\(y=3x^{2}\)です。 このように、係数\(a\)が正のときは上が開いた形に、負のときは下が開いた形となります。 より詳しく知りたい方は→中3数学y=ax^2のグラフってどんな形になるの?いくつかの特徴につい
Y=ax二乗のグラフのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  |  |
「Y=ax二乗のグラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「Y=ax二乗のグラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「Y=ax二乗のグラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「Y=ax二乗のグラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
「Y=ax二乗のグラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
「Y=ax二乗のグラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「Y=ax二乗のグラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「Y=ax二乗のグラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「Y=ax二乗のグラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「Y=ax二乗のグラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「Y=ax二乗のグラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 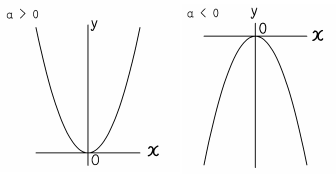 | |
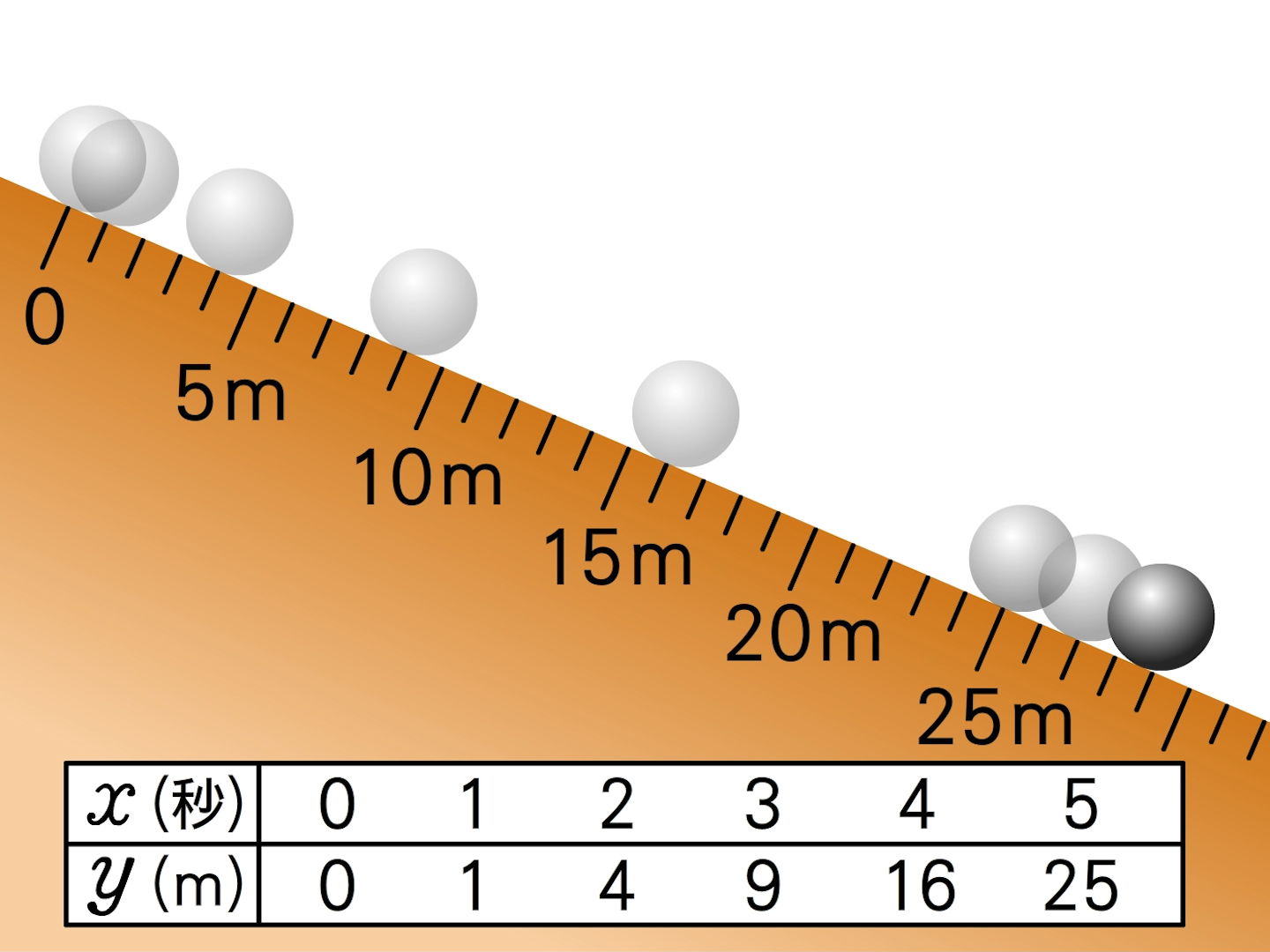 | 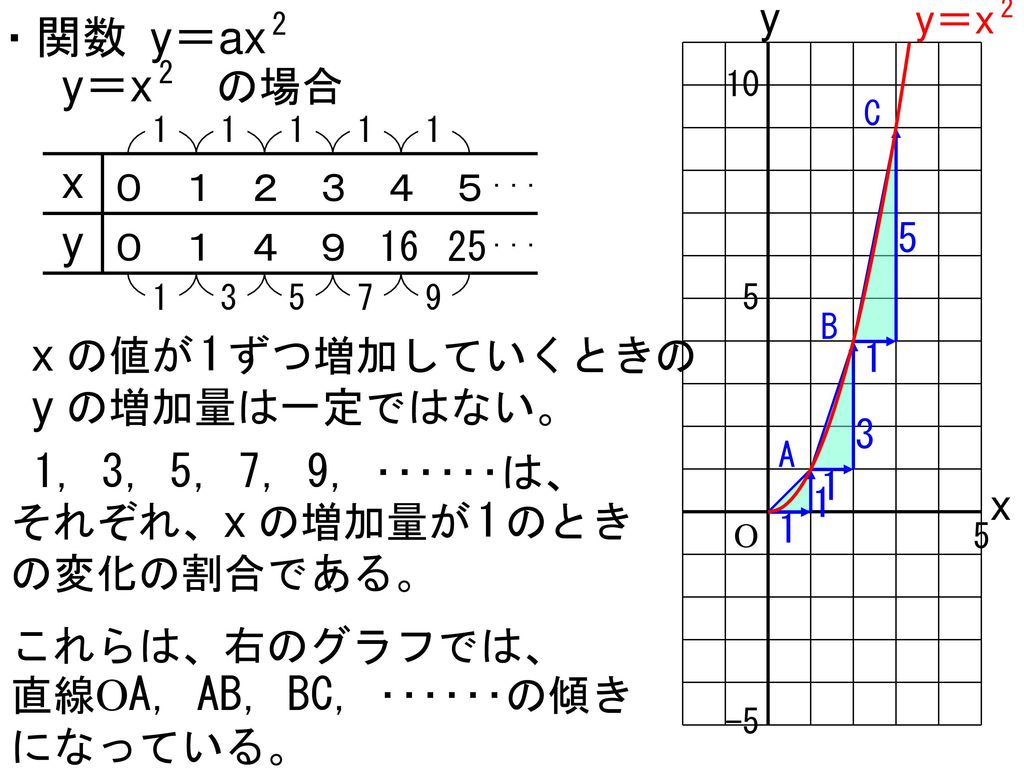 |
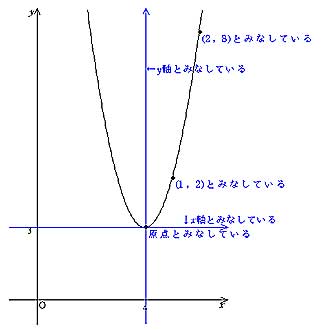
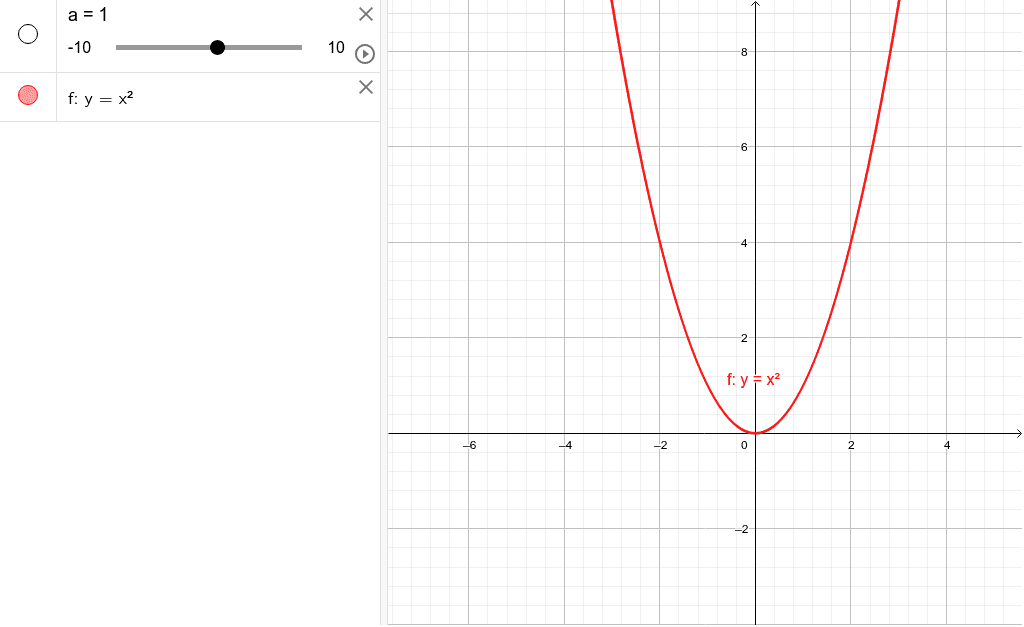
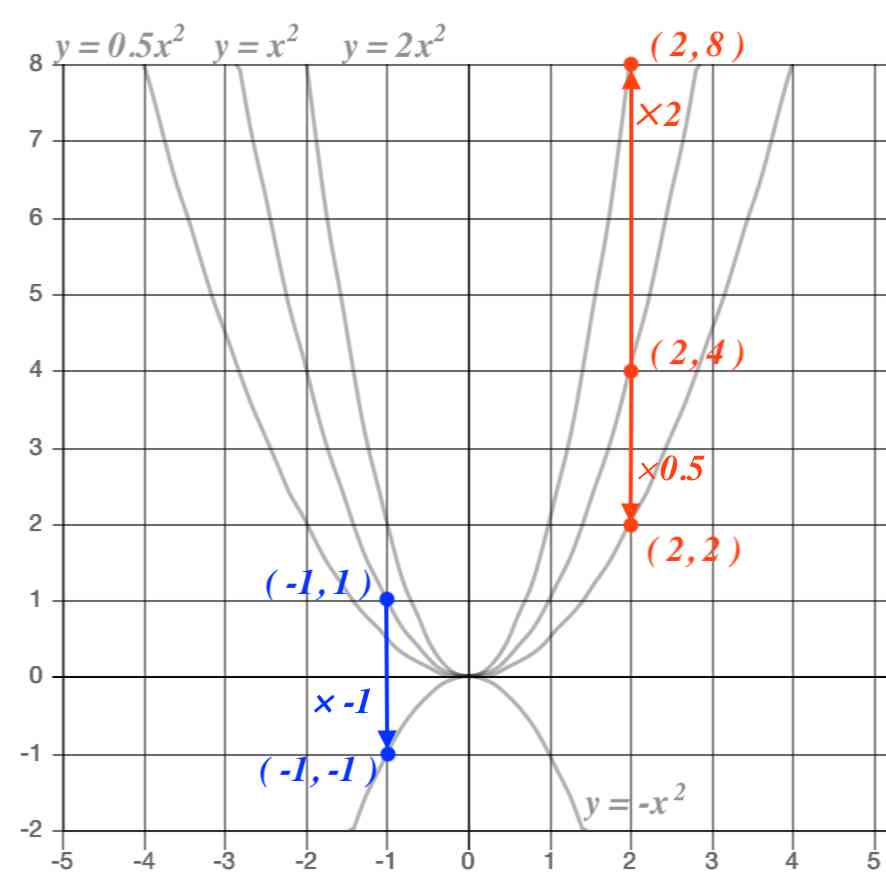
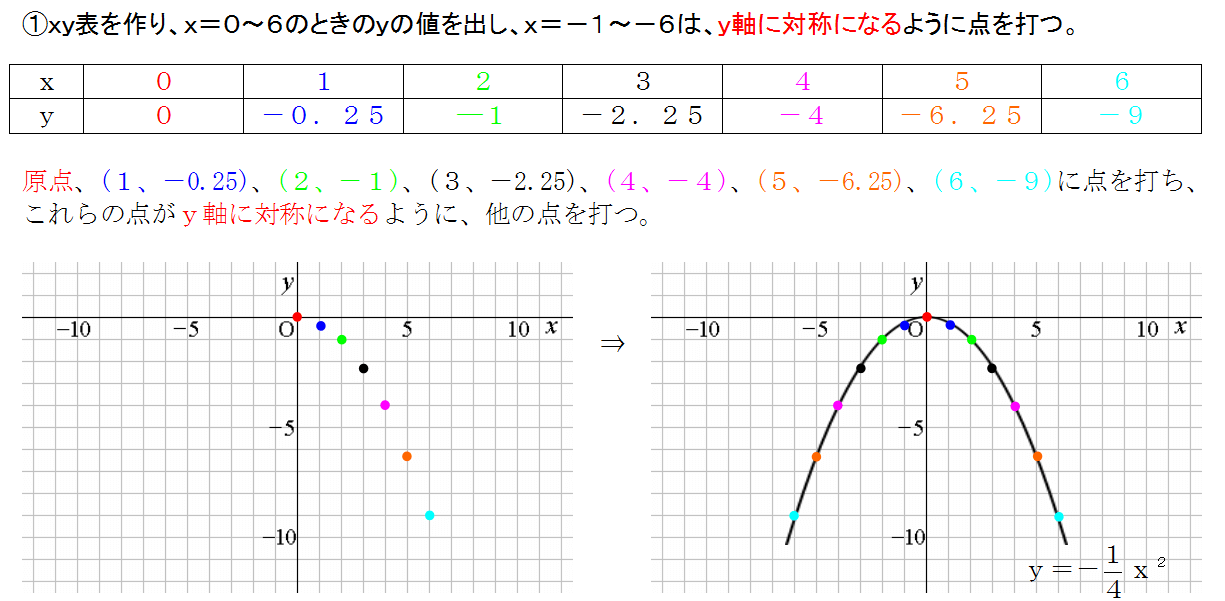
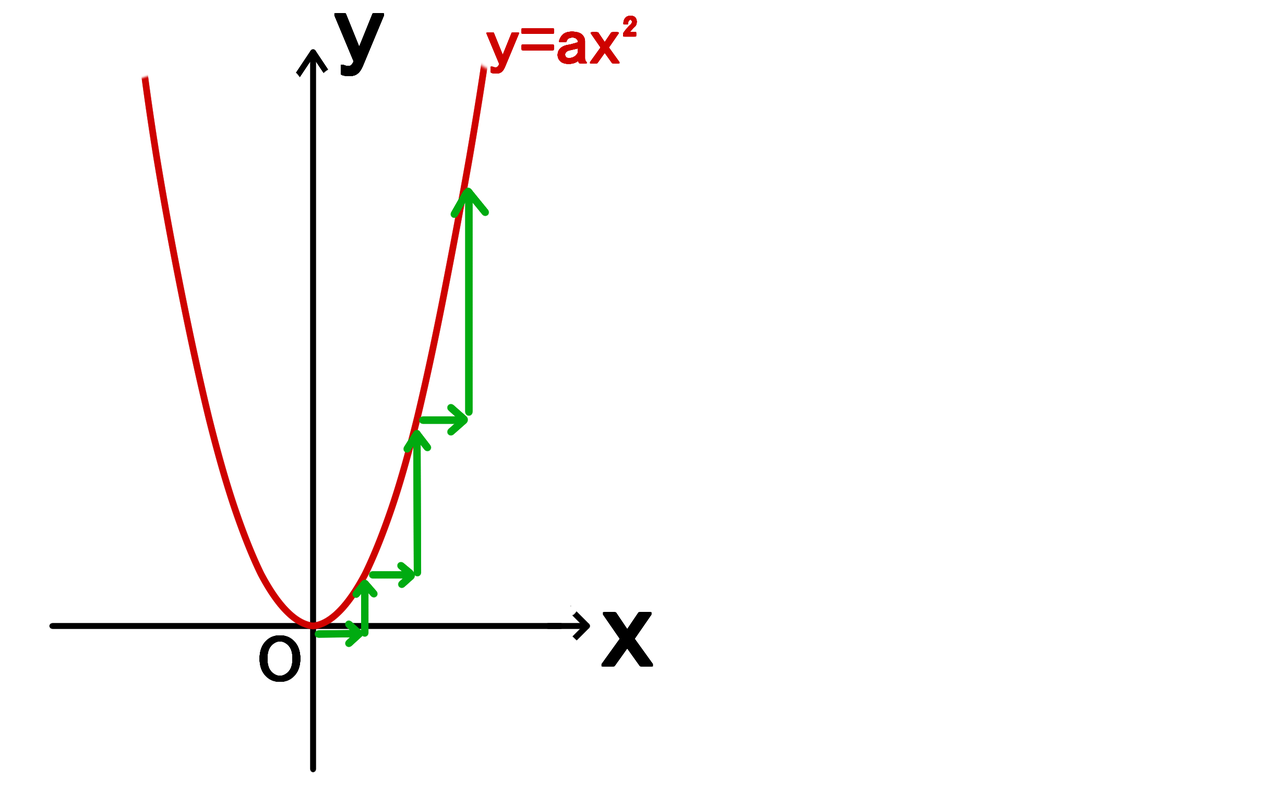
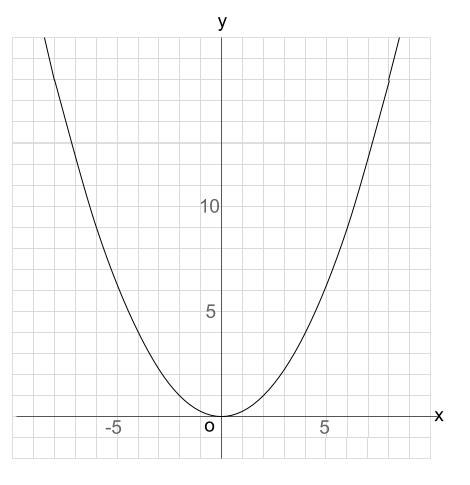
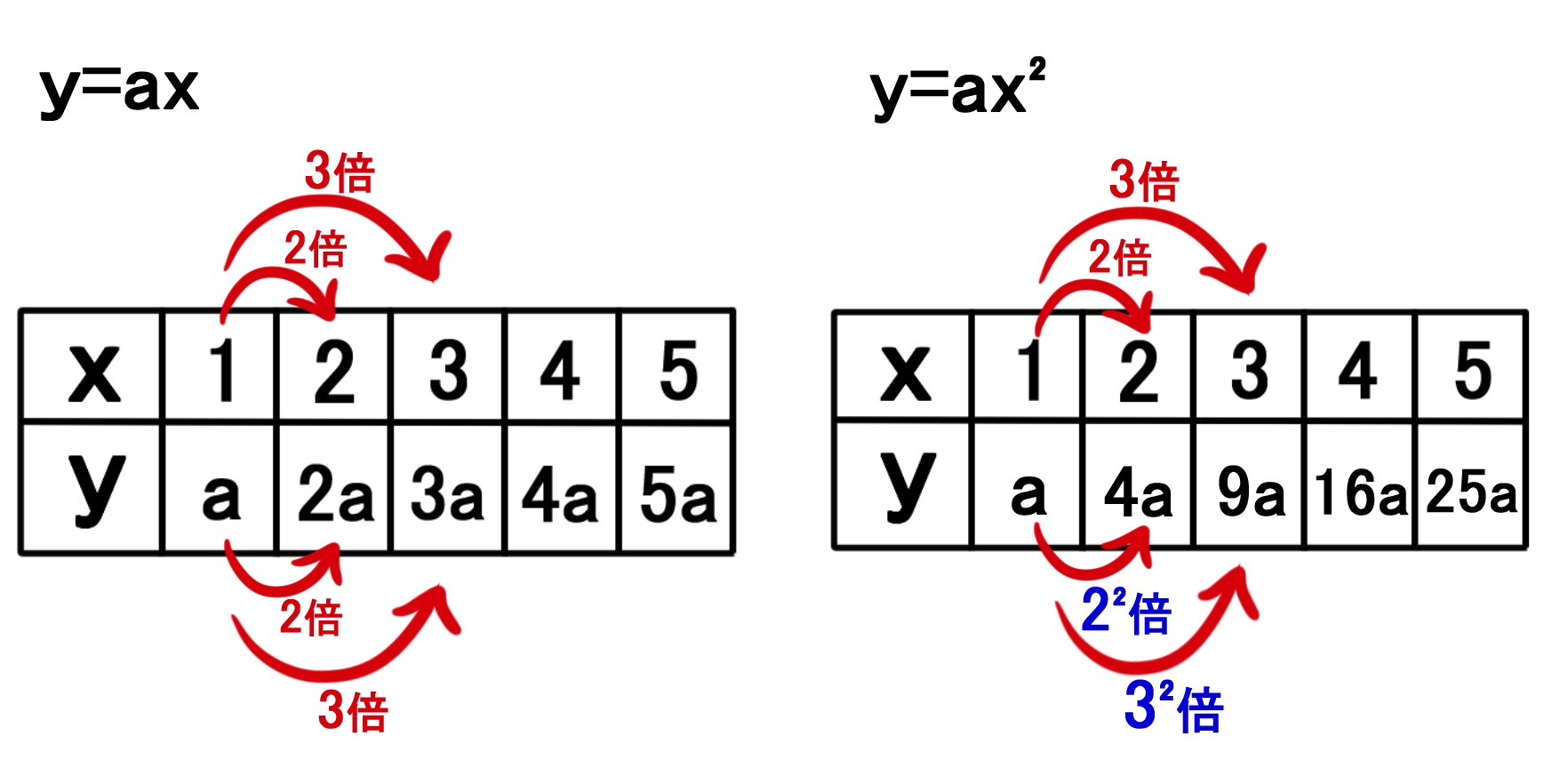
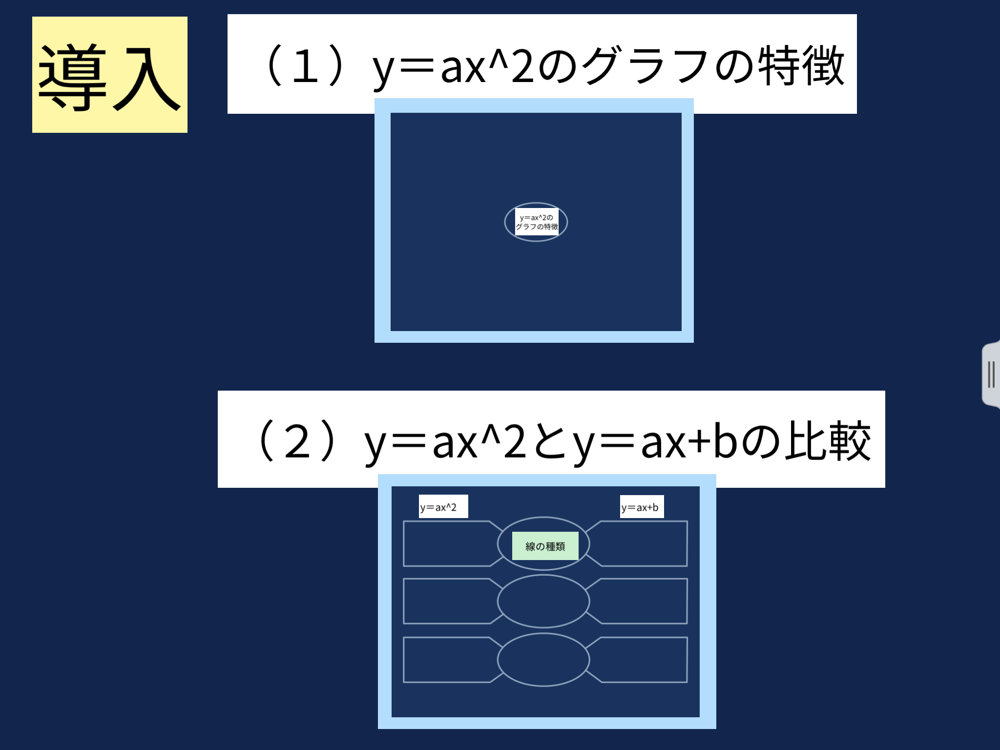
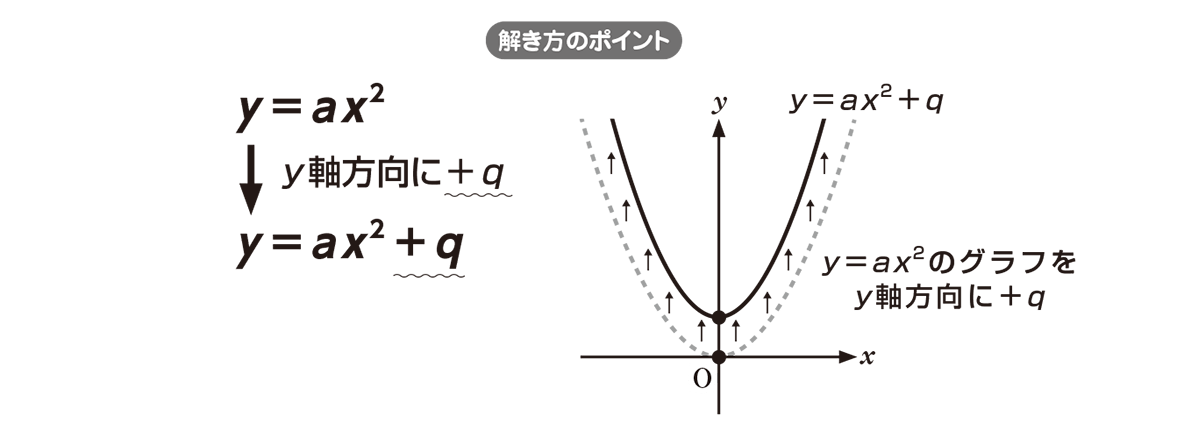
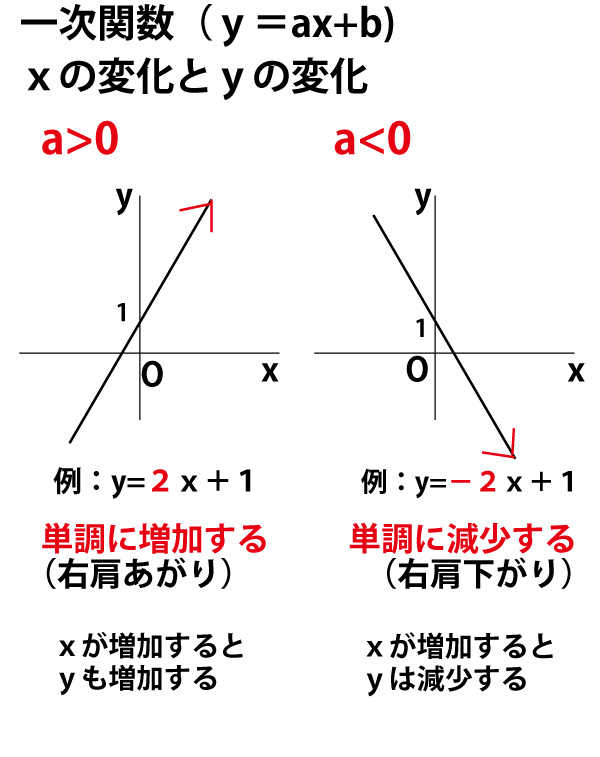
Y=ax 2 のグラフの特徴 必ず原点を通り、その原点が頂点である。 y軸について対称である。 a > 0のときは上に開き、a < 0のときは下に開く。 aの絶対値が小さいほどグラフの開きが大きい。 y=ax 2 のグラフとy=ax 2 のグラフはx軸について対象である。 二次関数嫌いの先入観を解消するには、「 二次関数は一次関数から1つ増えただけ 」と思うことが大切です。 一次関数を発展させたのが二次関数です。 一次関数は、例えば「 y=ax 」です。 a に「 2 」を入れれば「 y=2x 」になります。 これが簡単なのは、「 y は x の 2 倍」とすぐに





0 件のコメント:
コメントを投稿